Pair of Angles

According to angle sum property, the sum of angles in any triangle is 

Prove that the sum of all interior  angles of a quadrilateral $ABCD$ is $360°$.

Show that, there is only one perpendicular drawn to a line from the external point (point not on it).

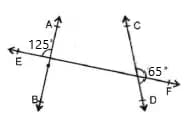
When two lines $\mathrm{AB} \mathrm{and} \mathrm{CD}$ intersects at a point $\mathrm{O}$ as shown in the figure. Then prove that, the pair of vertically opposite angles formed by the lines are equal.

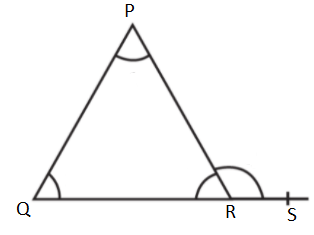
Prove that $\angle PRS=\angle P+\angle Q$, as shown in the given triangle $PQR$.

In figure, to prove that $\mathrm{AB}\parallel \mathrm{CD}$.

Identify whether the given statement "The whole is greater than a part" is a conjecture, axiom or theorem.

Identify whether the given statement "Things which coincide with one another are equal to one another" is a conjecture, axiom or theorem.

Identify whether the given statement "Things which are equal to the same thing are equal to one another" is a conjecture, axiom or theorem.

The supplement of $63°36\text{'}40\text{'}\text{'}$ is

The complement of $52°27\text{'}38\text{'}\text{'}$ is

The complement of $33°21\text{'}46\text{'}\text{'}$ is

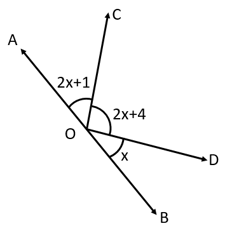
Find the value of $x$ in the following figure.

Find $x$ in the following figure.

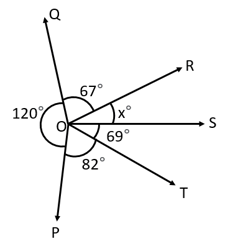
Find the angle which is $24°$ less than its supplement.

Find the supplementary angle of $\frac{3}{7}$ of $280°$.

Prove the following theorem.

The perpendicular from the centre of the circle to a chord bisects the chord. 

Prove the following theorem.

If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal.

Prove the following theorem.

Equal chords of a circle subtend equal angles at the centre.

Prove the following theorem.

The sum of the interior angles of a triangle is $180°$.